Abstract¶
TACO is a toolsuite for the development and automatic verification of fault-tolerant and threshold-based distributed algorithms, for example, byzantine consensus protocols, modeled as threshold automata (TA).
Currently, TACO implements three model checkers for threshold automata, two of which can also be used for the verification of so called extended threshold automata (ETA). It can be used as a completely push-button tool - supply it with a TA and a specification, and it will automatically choose a model checking algorithm and check whether the specification is satisfied. This allows you to verify threshold automata (and distributed algorithms in general) even if you are not an expert.
Additionally, TACO is a modular, extensible, and well-documented framework for developing algorithms and tools for threshold automata. All of TACO’s components are openly available and ready to use on crates.io.
Welcome to the documentation of the Threshold Automata for COnsensus (TACO) toolsuite!
Organization of the Documentation¶
TACOs documentation contains three main sections:
Theoretical Background gives an introduction to the threshold automaton model as well as a brief introduction to the different specification formats supported by TACO. Additionally, it contains a high-level overview of the model checking algorithms implemented in TACO.
User Guide CLI describes how to use the TACO CLI for model checking and also contains more details on TACO’s input formats.
Developer Documentation gives an overview of the crates of TACO and serves as an entrypoint to the documentation of the TACO internal APIs. Additionally it contains setup instructions for a development environment for working on the TACO source code.
High-Level Architecture of TACO¶
TACO consists of representations for different flavors of so called Threshold Automata (TA) 1 (see Theoretical Background), on different abstraction levels, back-end components such as a unified interface to binary decision diagram (BDD) libraries and satisfiability modulo theories (SMT) solvers, three model checker implementations, as well as utility code, e.g., a parser for specification files or the command line interface (CLI).
All components are designed to be usable individually to enable fast and easy development of, for example, new model checking algorithms, different user interfaces, new specification formats or testing of new backends like a new BDD library. A high-level overview of the architecture is provided in Figure 1.
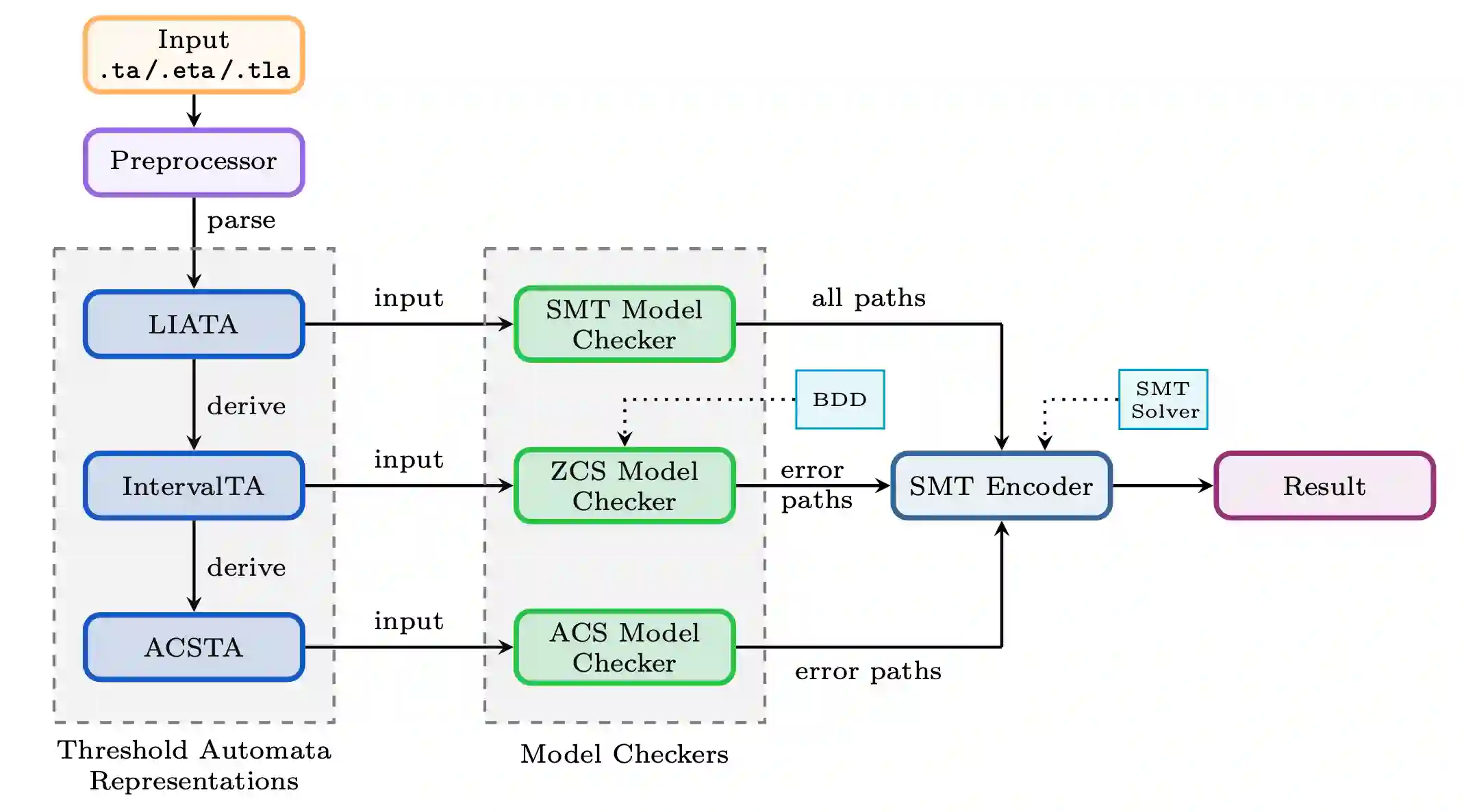
Figure 1:Architecture of the TACO toolsuite.
Tool Features¶
Features for Algorithm Designers¶
Algorithm designers do not only get a yes/no answer whether the current protocol satisfies the specification but can get various other outputs. Firstly, for more intuitive modeling and verification, TACO supports the visualization of TA. Additionally, if an error is found during verification, a concrete error trace is printed that points to the problem in the current design. You can also choose whether a compact representation of error paths should be printed, which omits locations with 0 processes and variables that are 0. Finally, the two algorithms that construct error graphs can produce helpful intermediate results in the form of abstract error paths even if these are spurious, they can help you to amend the protocol to remove bugs or to make it more easily verifiable.
Features for Formal Methods Experts¶
While TACO can be used as a push-button tool, based only on an input TA and a specification, its behavior can be guided through a wealth of parameters.
First, you can of course choose which of the three model checking algorithms to use. Moreover, TACO allows for the fine-grained configuration of the underlying SMT solvers and BDD managers, for example, to choose SMT solving heuristics. For specifications composed of multiple properties, you can choose whether TACO should terminate after finding the first violation or whether it should continue until all properties are verified.
Additionally, the ZCS approach can optionally be used as a heuristic that only tries to verify safety by checking if the error graph is empty. This check over-approximates the possible behaviors of the TA, but it can be much more efficient than a full model checking run.
Extensions of the System Model¶
TACO goes beyond the decidable fragment of threshold automata 12. It is the first tool to support extended threshold automata (ETAs) 13 that also allow for variable decrements and resets. Of course, TACO is not guaranteed to terminate for such inputs. Still, our experiments indicate that it can be a useful tool for algorithms that need the expressivity.
Preprocessing¶
When given a threshold automaton uses a static analysis of the TA and the specification to simplify the problem and remove unnecessary locations and variables. This includes self-loops of the TA that do not have any effect (i.e., they do not change the value of any variable), or transition guards that are trivial because they will always be satisfied for the given resilience condition specified in the TA.
Moreover, if TACO can statically determine that some locations are never reachable because they are empty initially and there are no incoming transitions from non-empty locations, then we completely remove these locations from the TA when checking the given property. Note that this may depend on the given specification, as it may specify that some of the initial locations should be empty.
Code Quality¶
The goal of a model checker is to verify the safety of a protocol, thereby increasing trust in its correctness. However, we still need to trust the verifier. While we have not proven the correctness of TACO in a proof assistant, TACO uses extensive testing (around 97% of line coverage at the time of writing) and uses software engineering best practices, such as code reviews and linting to maintain a (somewhat) trustworthy code base.
Additionally, TACO is written entirely in the safe fragment of Rust (simply called safe Rust), guaranteeing memory and type safety while not adding major overhead and allowing for low-level optimizations.
Modularity¶
Our goal with the design of TACO was not only to provide an efficient implementation of model checking algorithms but also to enable others to write tools for threshold automata. In this spirit, we designed TACO in a highly modular fashion.
Most major components, such as parser and preprocessor, or different TA representations and model checking algorithms, are separated into individual Rust crates, and specific features are guarded by feature flags. This design for example allows you to easily create a new user interface by integrating the parser and one of the model checkers while not importing our CLI and the other model checking algorithms. Similarly, new specification formats can simply be implemented by implementing the existing parser trait.
The same modular approach has been taken for backend components such as SMT solvers or BDD libraries. TACO supports any SMT solver that uses the SMTLIB2 standard 4 and has an interactive mode. For BDD libraries we implemented a simple high-level interface, which requires minimal code to add a new library, and we currently support CUDD 5 and OxiDD 6.
Please feel free to use TACO and all of its components to build your own tools for threshold automata or integrate TACO with your SMT solvers or BDD libraries. The Developer Documentation should provide you with all the details on TACO’s components and enable you to set up a development environment.
- Konnov, I., Veith, H., & Widder, J. (2014). On the Completeness of Bounded Model Checking for Threshold-Based Distributed Algorithms: Reachability. In P. Baldan & D. Gorla (Eds.), CONCUR 2014 - Concurrency Theory - 25th International Conference, CONCUR 2014, Rome, Italy, September 2-5, 2014. Proceedings (Vol. 8704, pp. 125–140). Springer. 10.1007/978-3-662-44584-6_10
- Kukovec, J., Konnov, I., & Widder, J. (2018). Reachability in Parameterized Systems: All Flavors of Threshold Automata. In S. Schewe & L. Zhang (Eds.), 29th International Conference on Concurrency Theory, CONCUR 2018, September 4-7, 2018, Beijing, China (Vol. 118, p. 19:1-19:17). Schloss Dagstuhl - Leibniz-Zentrum für Informatik. 10.4230/LIPICS.CONCUR.2018.19
- Baumeister, T., Eichler, P., Jacobs, S., Sakr, M., & Völp, M. (2024). Parameterized Verification of Round-Based Distributed Algorithms via Extended Threshold Automata. In A. Platzer, K. Y. Rozier, M. Pradella, & M. Rossi (Eds.), Formal Methods - 26th International Symposium, FM 2024, Milan, Italy, September 9-13, 2024, Proceedings, Part I (Vol. 14933, pp. 638–657). Springer. 10.1007/978-3-031-71162-6_33
- Barrett, C., Stump, A., Tinelli, C., & others. (2010). The SMT-LIB standard: Version 2.0. Proceedings of the 8th International Workshop on Satisfiability Modulo Theories (Edinburgh, UK), 13, 14.
- Somenzi, F., Bahar, I., Cho, H., Frohm, E., Gaona, C., Hua, C., Jang, J.-Y., Jeong, S.-W., Kumthekar, B., Macii, E., Manne, B., Moon, I.-H., Musfeldt, C., Panda, S., Pardo, A., Ravi, B. P. K., Shin, H., Shuler, A., Sivakumaran, A., & Sivesind, J. (unknown). CUDD: CU Decision Diagram Package (unkown, Ed.). https://github.com/cuddorg/cudd
- Husung, N., Dubslaff, C., Hermanns, H., & Köhl, M. A. (2024). OxiDD: A Safe, Concurrent, Modular, and Performant Decision Diagram Framework in Rust. Proceedings of the 30th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS’24). 10.1007/978-3-031-57256-2_13